Vi
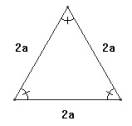
tar nå utgangspunkt i en likesidet trekant
der
sidelengdene er 2a.
Obliagtorisk
innleveringsoppgave i Matematikk 1
Dette er en obligatorisk innleveringsoppgave i matematikk. Dere skal
levere den inn til faglærer og få den tilbake med kommentarer, rettinger –
ikke karakter.
Oppgaven skal leveres individuelt. Innleveringsfristen er 09.april 2003.
OPPGAVE 1 (Eksamen i lærerutdanning
H2001)
|
Vi
tar nå utgangspunkt i en likesidet trekant der
sidelengdene er 2a. |
|
(a) Hva er høyden i denne trekanten? (Finn et
uttrykk for høyden uttrykt ved a.)
(b) Hva er høyden i en pyramide med kvadratisk
bunn, der veggene er likesidede trekanter med sidelengde 2a? (Vis hvordan
du kommer fram til et uttrykk for høyden i pyramiden uttrykt ved variabelen a.)
|
Et
oktaeder er satt sammen av åtte likesidede trekanter, dvs som to
pyramider med kvadratisk bunn der pyramidenes bunnflater er satt mot
hverandre. |
|
(c) Vi ser på et oktaeder som er satt sammen av
8 likesidede trekanter med sidelengde 2a. Du skal nå finne avstanden
mellom to hjørner som ligger lengst mulig fra hverandre i dette oktaederet. Vis
hvordan vi kommer fram til samme uttrykk for denne avstanden på to måter:
(i)
- ved å
bruke resultatet du kom fram til i oppgave (b).
(ii)
- uten å bruke resultatet du kom fram til i oppgave (b).
OPPGAVE 2 (Eksamen i lærerutdanning Vår 2000)
Kari
kjøper en ny bil i året 2000. Den koster 230000 kr. Hun lager en modell for
utviklingen av verdien av denne bilen. Denne modellen er basert på jevn
prosentvis nedgang. I løpet av 2 år er nedgangen 40 %.
a) Regn ut verdien av bilen for årene 2002, 2004, 2006, 2008. Bruk disse resultatene og tegn ei kurve for verdien av bilen i et koordinatsystem. La 1 cm på x-aksen tilsvare 1 år og 1 cm på y-aksen tilsvare 10000 kr. (Bruk det ordinære innføringsarket med rutemønster)
b) Bruk tegninga og les av:
1)
Hvor mye er bilen verdt i året 2005?
2)
Når er bilen verdt 100000 kr?
c)
La x være antall år etter år 2000. La f(x) være verdien av bilen x år
etter 2000 i følge Karis modell. Forklar hvorfor verdien av bilen er en
funksjon av alderen.
Finn et funksjonsuttrykk for f(x) for Karis modell.
Kari antar at levetida til bilen er 15 år. Bruk dette til å gi en fornuftig
definisjonsmengde og verdimengde til f.
d) Følgende påstander om verdien av brukte biler er hevda:
Påstand 1: Verdien av en bil vil avta mest ( i
kroner) det første året
Påstand 2: En bil vil gå ned 20 % i verdi det første
året.